Value Function Approximation

Part II

Reference: Sutton and Barto, Chapter 9-11

Table of Contents


  • Batch Reinforcement Methods

  • Least Squares Policy Iteration(LSPI)

Batch Reinforcement Methods

Batch Reinforcement Methods


  • Gradient descent is simple and appealing

  • But it is not sample efficient

  • Batch methods seek to find the best fitting value function

  • Given the agent’s experience (“training data”)

Least Squares Prediction

Multi-armed Bandit

Stochastic Gradient Descent with Experience Replay

Multi-armed Bandit

Experience Replay in Deep Q-Networks (DQN)

Multi-armed Bandit

DQN in ATARI

The model

Multi-armed Bandit

Performance

Multi-armed Bandit

Benefits of Experience Replay and Double DQN

Multi-armed Bandit

DQN Example and Code

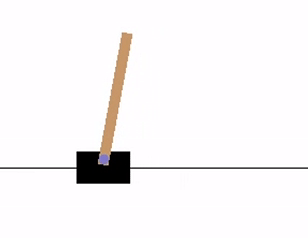
Multi-armed Bandit

CartPole Example

The agent has to decide between two actions - moving the cart left or right - so that the pole attached to it stays upright.

State Space

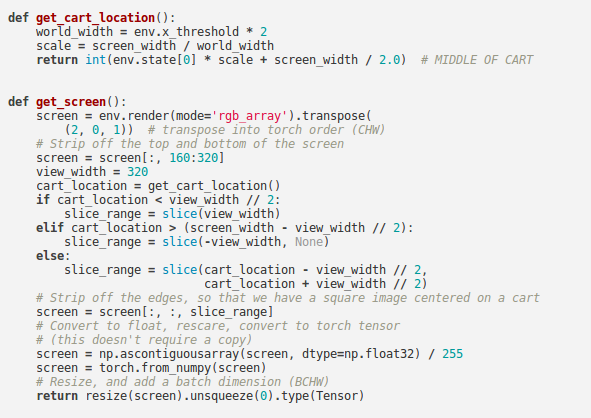
State is the difference between the current screen patch and the previous one. This will allow the agent to take the velocity of the pole into account from one image.

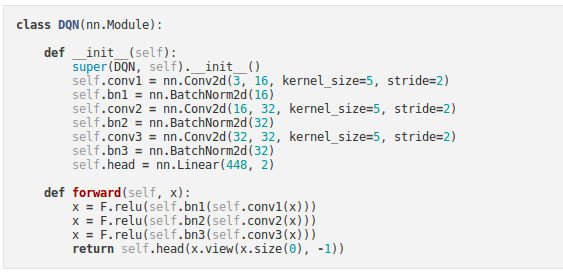
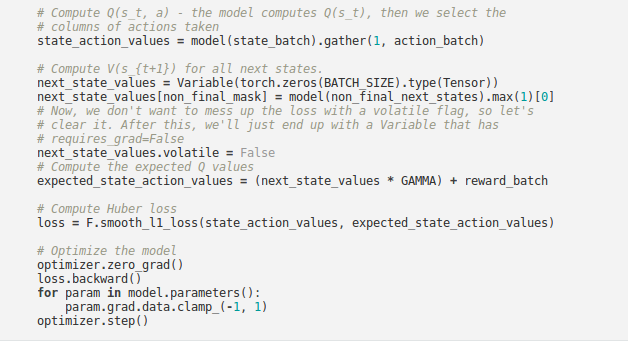
Q-network
  • Our model will be a convolutional neural network that takes in the difference between the current and previous screen patches.
  • It has two outputs, representing Q(s,left) and Q(s,right) (where s is the input to the network).
  • In effect, the network is trying to predict the quality of taking each action given the current input.
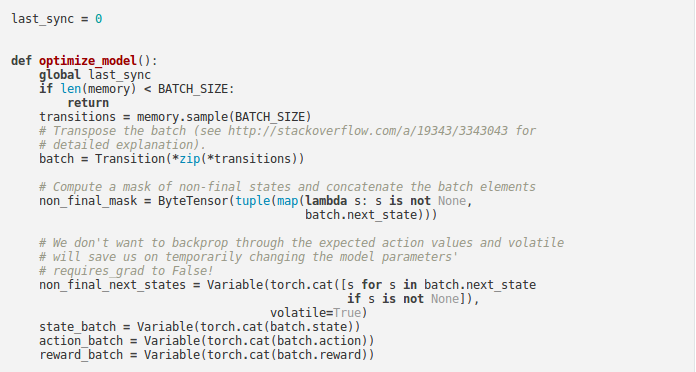
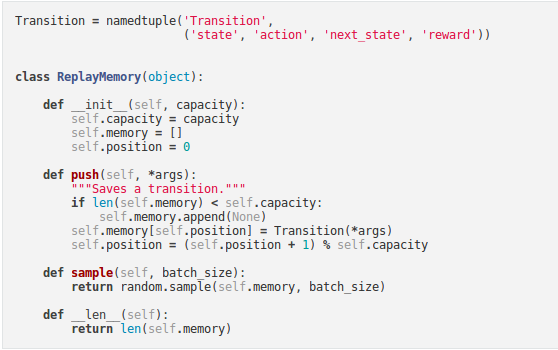
    Multi-armed Bandit
Replay Memory
  • Experience replay memory is used for training the DQN.
  • It stores the transitions that the agent observes, allowing us to reuse this data later.
  • By sampling from it randomly, the transitions that build up a batch are decorrelated.
  • It has been shown that this greatly stabilizes and improves the DQN training procedure.
    Multi-armed Bandit
Input Extraction

How do we get the crop of the cart?

Multi-armed Bandit
Selecting an Action

This is done based on $\epsilon$ greedy policy.

Multi-armed Bandit
Training
Multi-armed Bandit
Multi-armed Bandit
Multi-armed Bandit

Linear Least Squares Prediction

Linear Least Squares Prediction



  • Experience replay finds least squares solution

  • But it may take many iterations

  • Using linear value function approximation $\hat{v}(s, w) = x(s)^Tw$

  • We can solve the least squares solution directly

Linear Least Squares Prediction

Multi-armed Bandit

Linear Least Squares Prediction Algorithms

Multi-armed Bandit
In [ ]:

Linear Least Squares Prediction Algorithms

Multi-armed Bandit

Least Squares Policy Iteration(LSPI)

Multi-armed Bandit

Least Squares Action-Value Function Approximation

Multi-armed Bandit

Least Squares Control

Multi-armed Bandit

Least Squares Q-Learning

Multi-armed Bandit

Least Squares Policy Iteration(LSPI) Algorithm

Multi-armed Bandit