Finite Markov Decision Processes

Reference: Chapter 3, Sutton and Barto

Contents

• Introduction

• Building Blocks of MDP
  • Markov Property
  • Episodic vs Continuous Tasks
  • State Transition Matrix
  • Return
  • Discount
  • Value Function

• MDP Parameters
  • Policy in MDP notations
  • Value Functions in MDP notations

• Bellman Expectation Equations

• Bellman Optimal Equations

The Agent Environment Interface

• At each time step t,
  • the agent has some representation of the environment’s state, $S_t \in S$,
    • where S is the set of possible states,

• On basis of $S_t$,agent selects an action, $A_t \in A(S_t)$,
  • where $A(S_t)$ is the set of actions available in state $S_t$.

• One time step later, as a consequence of its action,
  • the agent receives a numerical reward, $R_{t+1} \in R \subset R$, and
  • finds itself in a new state, $S_{t+1}$.

A very Flexible Framework

• The time steps can be any unit, non-fixed intervals of real-time;
  • Tracking: decision is per time step
  • Inventory management RL agent: Based only on current inventory state, time for depletion may vary.

• Actions can be low-level controls,or High-level Decisions
  • The voltages applied to the motors of a robot arm
  • Whether or not to have lunch or to go to graduate school.

• The states can take a wide variety of forms:
  • determined by low-level sensations, such as direct sensor readings,
  • high-level and abstract, such as symbolic descriptions of objects in a room.

• State could be based on memory of past sensations or even be entirely mental or subjective.

Some Key Points

• Boundary between agent and environment:not necessarily the same as the physical boundary of a robot’s or animal’s body.
  • The agent–environment boundary represents the limit of the agent’s absolute control, not of its knowledge.

• The reward signal Should communicate what you want it to achieve, not how you want it achieved.
  • Reward is placed outside the agent, so that it cant explicitly change reward formulation without achieving the goals.

• The state signal should not be expected to inform the agent of everything about the environment,
  • The agent is not designed to be omniscient.
  • State can contain, a copy of reward, part memory etc.

Building Blocks of MDP

Markov Property

“The future is independent of the past given the present”

• The state captures all relevant information from the history
• Once the state is known, the history may be thrown away
• i.e. The state is a sufficient statistic of the future

Markov State

• A state signal that succeeds in retaining all relevant information is said to be Markov, or to have the Markov property.
  • Checker Position
  • Location and Velocity of an Cannon ball

• If an environment has the Markov property,
  • one-step dynamics enable prediction of next state and expected next reward
  • based on current Action

• In such situation, the best policy for choosing actions as a function of a Markov state,
  • is just as good as the best policy for choosing actions as a function of complete histories.

• When state signal is non-Markov
  • We still approximate it as a markov process as,
  • We want our state representation to:
    • Be a good basis for predicting subsequent states,
    • Be a good basis for predicting future rewards, and
    • Be a good basis for selecting actions.

State Transition Matrix

Markov Process

Example

Example of Episodes

Example of Transition Matrix

Markov Reward Process

Example

Return

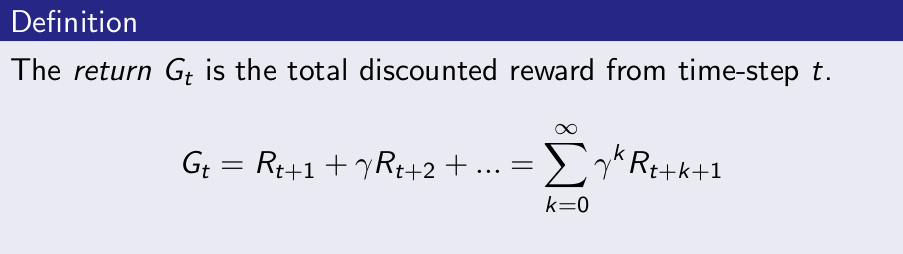
• The discount $γ ∈ [0, 1]$ is the present value of future rewards
• The value of receiving reward R after k + 1 time-steps is $γ^k R$.
• This values immediate reward above delayed reward.
  • $γ$ close to 0 leads to ”myopic” evaluation
  • $γ$ close to 1 leads to ”far-sighted” evaluation

Discount

Most Markov reward and decision processes are discounted. Why?

• Mathematically convenient to discount rewards
• Avoids infinite returns in cyclic Markov processes
• Uncertainty about the future may not be fully represented
• If the reward is financial, immediate rewards may earn more interest than delayed rewards
• Animal/human behaviour shows preference for immediate reward
• It is sometimes possible to use undiscounted Markov reward processes (i.e. $γ = 1$), e.g. if all sequences terminate.

Example

Value Function

The value function $v(s)$ gives the long-term value of state s

Example

Example

Example

Episodic vs Continuing Tasks

Episodic Tasks

• Each episode ends in a special state called the terminal state,
• Followed by a reset to a standard starting state or to a sample from a standard distribution of starting states.

Continuing Tasks

• The agent–environment interaction does not break naturally into identifiable episodes.
• It goes on continually without limit.

Unified Notation for Episodic and Continuous Tasks

Return for Episodic Tasks

sum over a finite number of terms

Return for Continuous Tasks

sum over an infinite number of terms

We need one convention to obtain a single notation that covers both episodic and continuing tasks.

How to do that?

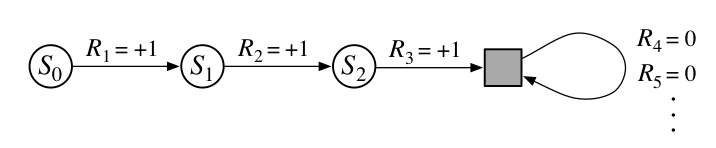
These can be unified by considering episode termination to be the entering of a special absorbing state that transitions only to itself and that generates only rewards of zero. For example, consider the state transition diagram -

Hence, return can be written as-

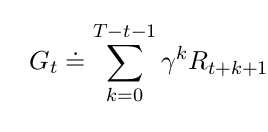
Markov Decision Process

Markov Decision Process

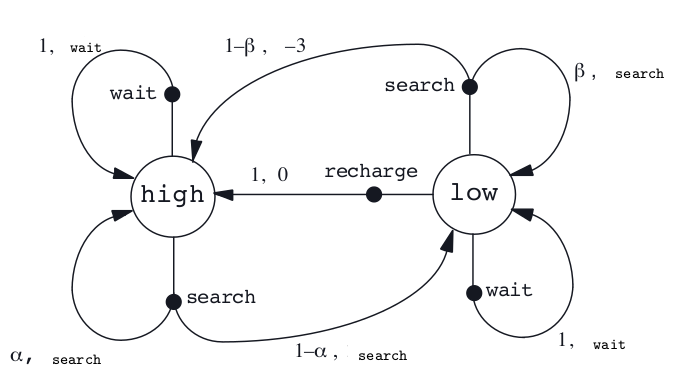
A Markov decision process (MDP) is a Markov reward process with decisions. It is an environment in which all states are Markov.

Policy in MDP notation

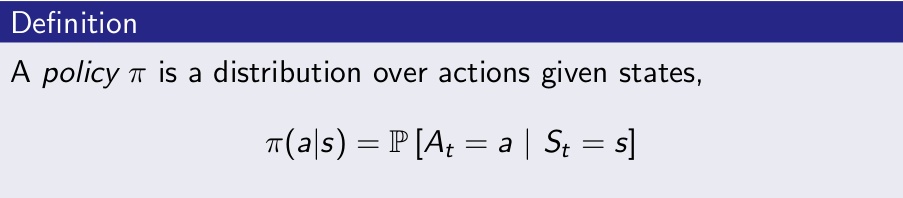
• A policy fully defines the behaviour of an agent
• MDP policies depend on the current state (not the history)
• i.e. Policies are stationary (time-independent), $A_t ∼ π(·|S_t ), \forall t > 0$

Policy in MDP notation

Given a MDP $M = \left \langle S, A, P, R, \gamma \right \rangle$ and a policy $\pi$

$$P_{s,s'}^{\pi} = \sum_{a \epsilon A} \pi(a|s) P_{ss'}^{a}$$$$R_{s}^{\pi} = \sum_{a \epsilon A} \pi(a|s) R_{s}^{a}$$

Example: Recycling Robot

Task:

Collect Empty soda cans in office

Sensors:

1) Detector : For detecting cans

2) Arm + Gripper : To pick up and place can in onboard bin

How can we formulate this as a MDP?

We first need to identify States (S), Actions (A) and Rewards (R)

Actions:

1) {Search} - Actively search for a can

2) {Wait} - Remain stationary and wait for someone to bring a can. (Will lose less battery)

3) {Recharge} - Head back home for recharging

States:

1) high - Battery is charged considerably well 2) low - Battery is not charged

Rewards:

1) zero most of the time

2) become positive when the robot secures an empty can,

3) negative if the battery runs all the way down

How can we now formulate this as a MDP?

Transition Probabilities and Expected Rewards

Transition Graph

Value Function in MDP notation

Bellman Expectation Equation

Bellman Expectation Equation

Bellman Expectation Equation for $V^\pi$

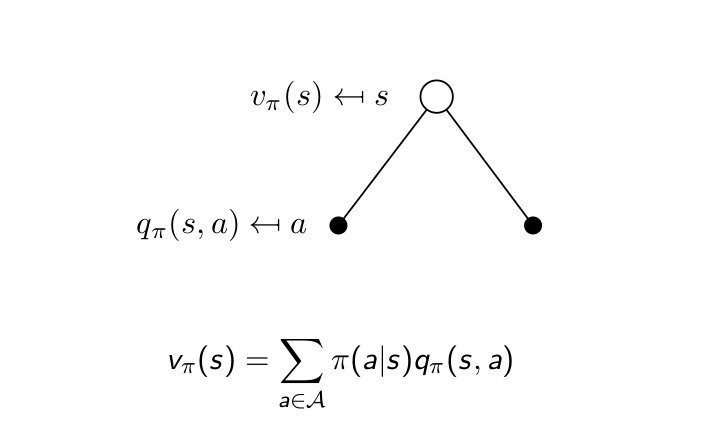
Bellman Expectation Equation for $Q^\pi$

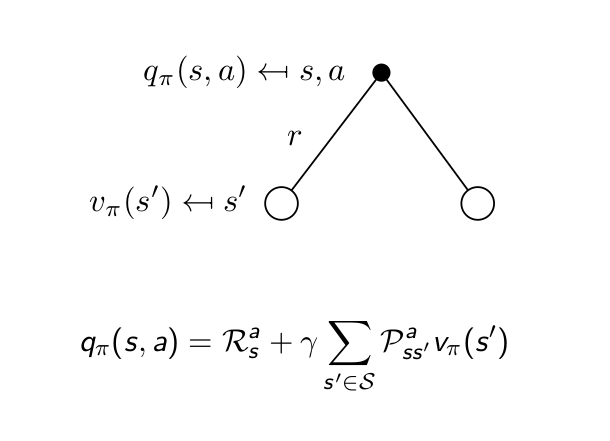
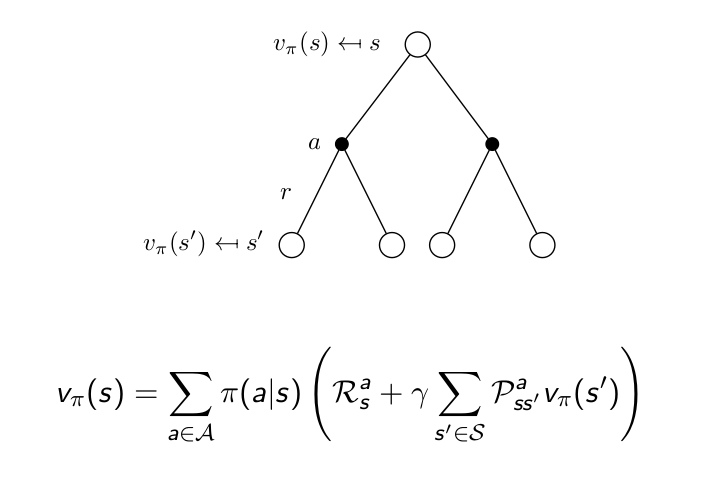
Bellman Expectation Equation for $v_\pi$

Bellman Expectation Equation for $q_\pi$

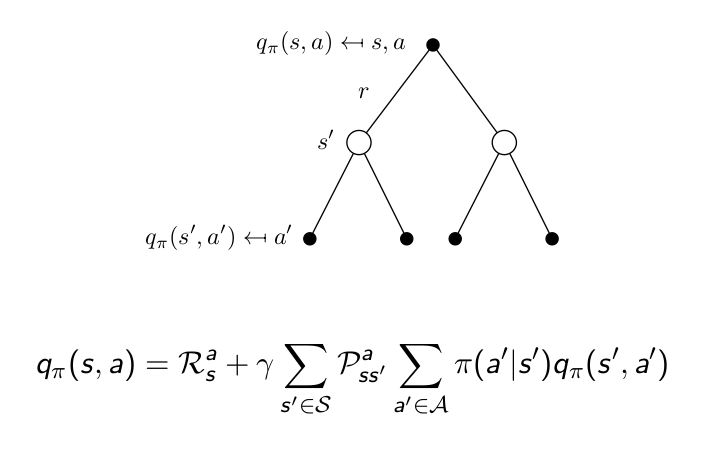
Bellman Optimality Equation

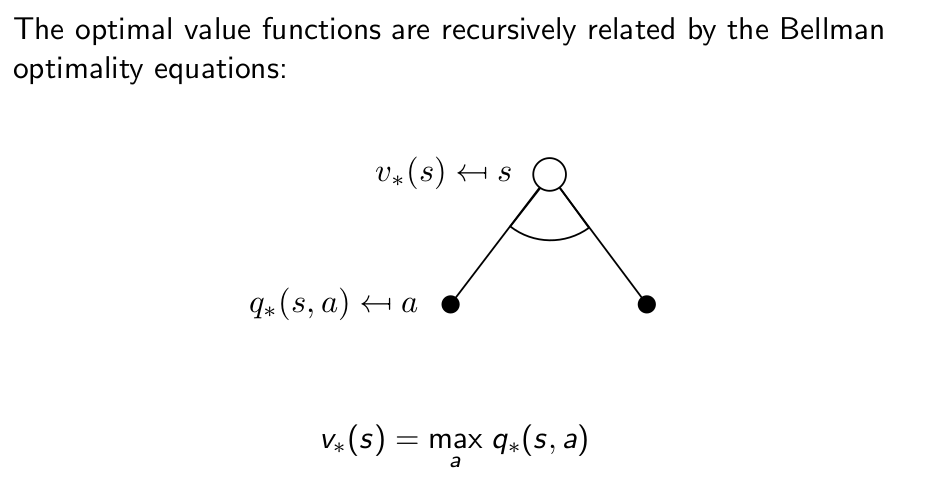
Optimal Value Function

Optimal Policy

Finding an Optimal Policy

Bellman Optimality Equation for $v_{*}$

Bellman Optimality Equation for $Q_{*}$

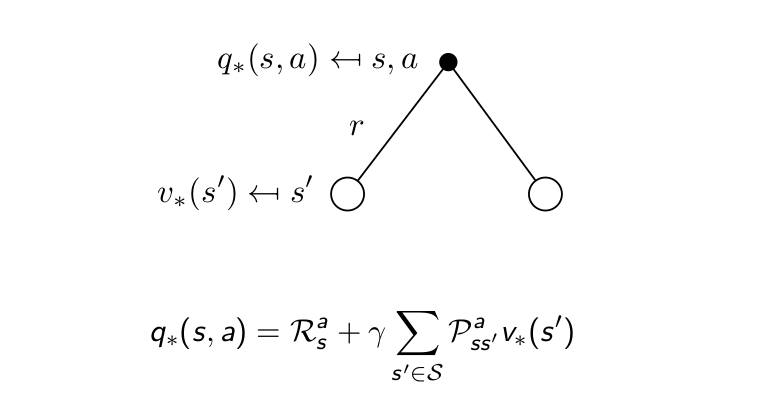
Bellman Optimality Equatin for $V^{*}$

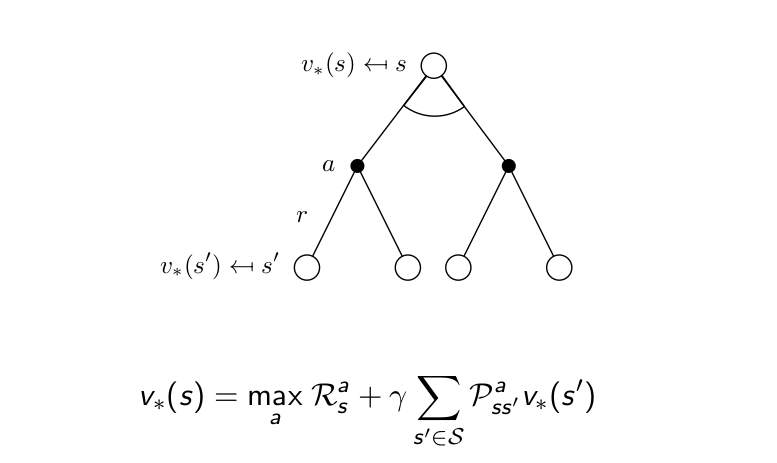
Bellman Optimality Equation for $Q^{*}$

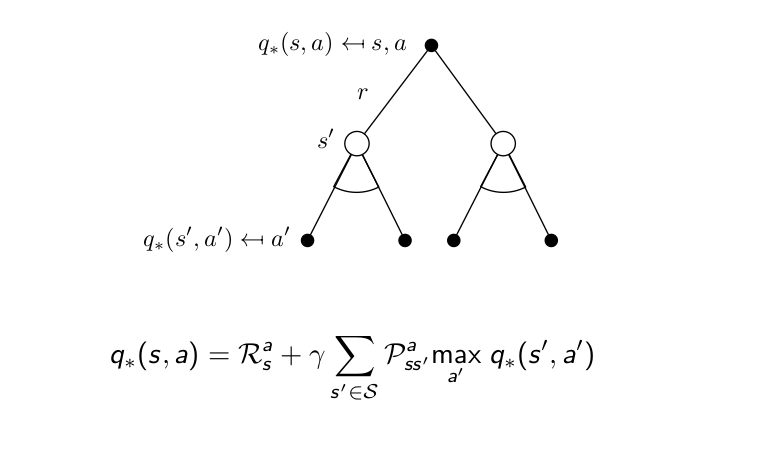
Summary

• We looked into the MDP formulation of a RL problem.
• We looked into the formulation of Value functions.
  • action-value pairs
  • state-action pairs
• Understood the motivation and necessity of Bellman Expectation Equations and Bellman Optimlality Equations