Monte Carlo Methods

Reference: Chapter 5, Sutton and Barto

Contents

  • Introduction
    • Why move to MCMC from DP?
  • Monte Carlo Prediction (On-Policy)
    • First-Visit Monte Carlo Policy Evaluation
    • Every-Visit monte Carlo Evaluation
  • Monte Carlo Estimation of Action Values
  • Monte-Carlo Control (On-Policy)
    • Building up on Generalised Policy Iteration
    • Issues with the method
      • a. Assuming Infinite number of episodes
      • b. Problem of “maintaining exploration”
    • Dealing with a. and b.
      • Two Solutions for Assumption a.
      • Ɛ-soft policies for Assumption b.
  • On-Policy vs Off-Policy Methods
  • Off-Policy MC Prediction
    • Problem Definition
    • Importance Sampling
  • Off-Policy MC Control

Introduction

  • Last Session we saw Dynamic Programming Approach to Solving MDPs
    • Policy Iteration
    • Value Iteration

  • Problem:

    • Assumed complete knowledge of the environment.
    • In many cases it is easy to generate experience sampled according to the desired probability distributions,
    • but infeasible to obtain the distributions in explicit form.

  • Can we use Experience instead for solving the MDP?

  • How to solve the MDP when we do not have complete knowledge of the environment?

  • Monte Carlo Methods: broad class of computational algorithms that rely on repeated random sampling to obtain numerical results.

  • Previously we computed value functions from knowledge of the MDP, here we learn value functions from sample returns with the MDP.

Monte-Carlo Prediction

Monte-Carlo Policy Evaluation

RewardHypothesis

First-Visit Monte-Carlo Policy Evaluation

RewardHypothesis

Pseudocode: First-visit MC Policy Evaluation

RewardHypothesis

Every-Visit Monte-Carlo Policy Evaluation

RewardHypothesis

Diference?

  • "These two Monte Carlo (MC) methods are very similar but have slightly different theoretical properties." - Sutton and Barto
  • Both have quadratic convergence to $v_\pi(s)$ with respect to $n$.

Incremental Monte-Carlo Updates

RewardHypothesis

Important Facts

  • The estimates from Monte Carlo methods for each state are independent.
    • The estimate for one state does not build upon the estimate of any other state,
    • In other words, Monte Carlo methods do not bootstrap.
  • We can learn value of only one or a subset of states.
    • We can generate many sample episodes starting from the states of interest,
    • Averaging returns from only these states ignoring all others

Monte Carlo Estimation of Action Values

Why compute action-values, instead of state-values?

  • If a model is not available: particularly useful to estimate action values q rather than state values v.
  • With model, state values alone are sufficient to determine a policy;
    • Simple one step looks ahead and
    • chooses action which leads to the best combination of reward and next state value.
  • Without model, however, state values alone are not sufficient.
    • Require explicitly estimate the value of each action for the values to be useful
    • Thus, one of our primary goals for Monte Carlo methods is to estimate $q_{∗}$ .

Complication with learning state-action values

Problem => Maintaining Exploration

Solution => Assumption of Exploring Starts

Exploring Starts

  • Every state-action pair has a nonzero probability of being selected as the start.
  • However, not always possible:
    • particularly when learning directly from actual interaction with an environment.
  • But very Useful when possible

Note: This assumption cannot be relied upon in general, particularly when learning directly from actual interaction with an environment. We will assume this and go ahead, and later explore how we can do away with this.

Monte Carlo Control

Generalised Policy Iteration (Refresher)

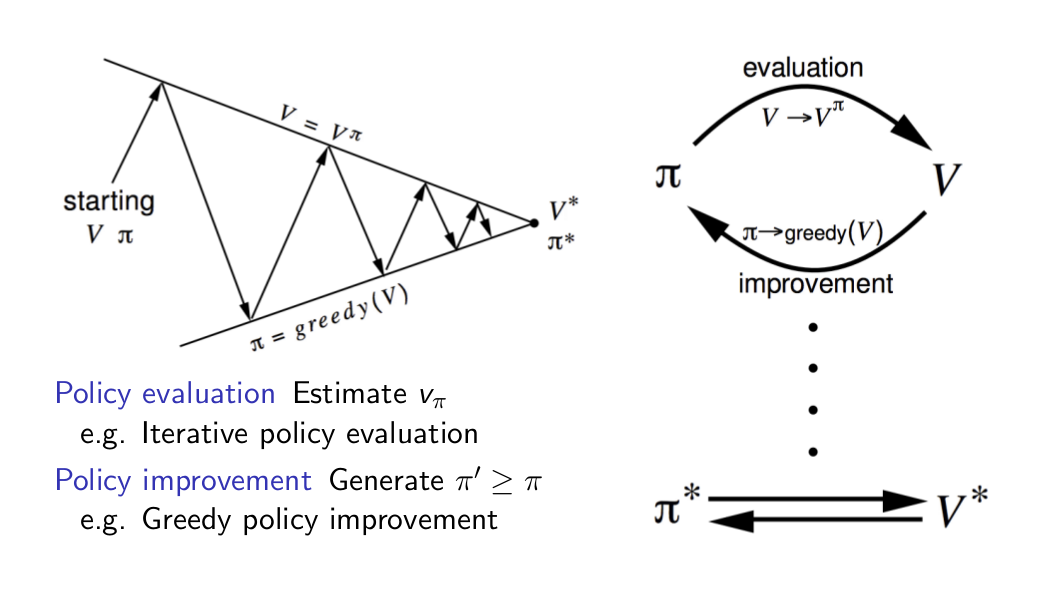
RewardHypothesis

Generalised Policy Iteration with Monte carlo Evaluation

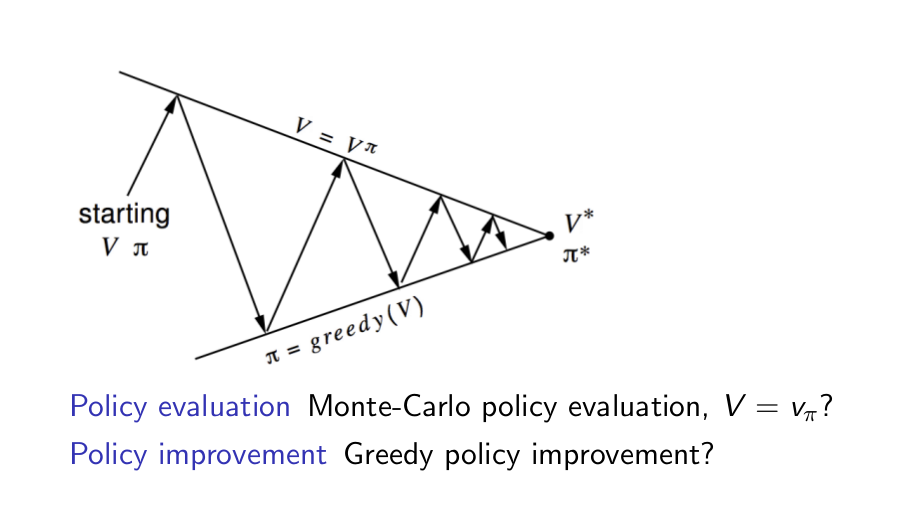
RewardHypothesis

Model-Free Policy Iteration Using Action-Value Function

RewardHypothesis

Generalised Policy Iteration with Action-Value Function

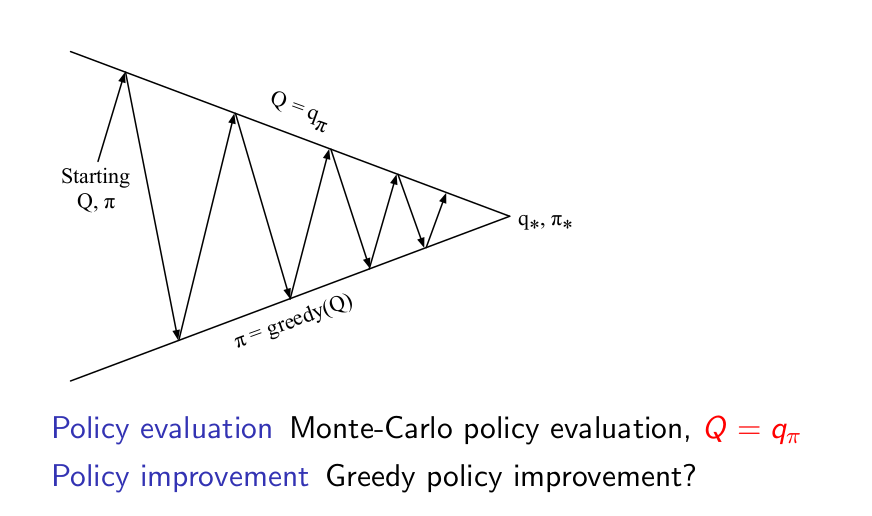
RewardHypothesis
Greedy Policy Improvement: $\pi(s) = argmax_{a} q(s,a)$

MC Control ES

RewardHypothesis

Assumptions in MC Control

1) Infinite Episodes for Learning

2) Exploring Starts Assumption

How to do without Infinite Episodes for learning?

  • Solution 1
    • Approximate $q_{\pi_k}$ in each policy evaluation.
    • Measurements and assumptions are made to obtain bounds on the magnitude and probability of error in the estimates,
    • Sufficient steps are taken during each policy evaluation to assure that these bounds are sufficiently small.
  • Solution 2
    • Forgo trying to complete policy evaluation before returning to policy improvement.
    • On each evaluation step we move the value function toward $q_{\pi_k}$, but we do not expect to actually get close except over many steps.
    • Extreme case: Value Iteration

How can you just assume Convergence?

"Convergence to this optimal fixed point seems inevitable as the changes to the action-value function decrease over time, but has not yet been formally proved. In our opinion, this is one of the most fundamental open theoretical questions in reinforcement learning"

  • Sutton and Barto, Reinforcement Learning: An Introduction(Draft).

How to do without Exploring Starts Assumption?

  • The only general way to ensure that all actions are selected infinitely often is that
    • the agent to continue to select them.
    • There are two approaches to ensuring this: on-policy methods and off-policy methods.

Monte Carlo Control without Exploring Starts (On-Policy)

$\epsilon$-Greedy Exploration

RewardHypothesis

$\epsilon$-Greedy Policy Improvement

RewardHypothesis

Monte-Carlo Policy Iteration

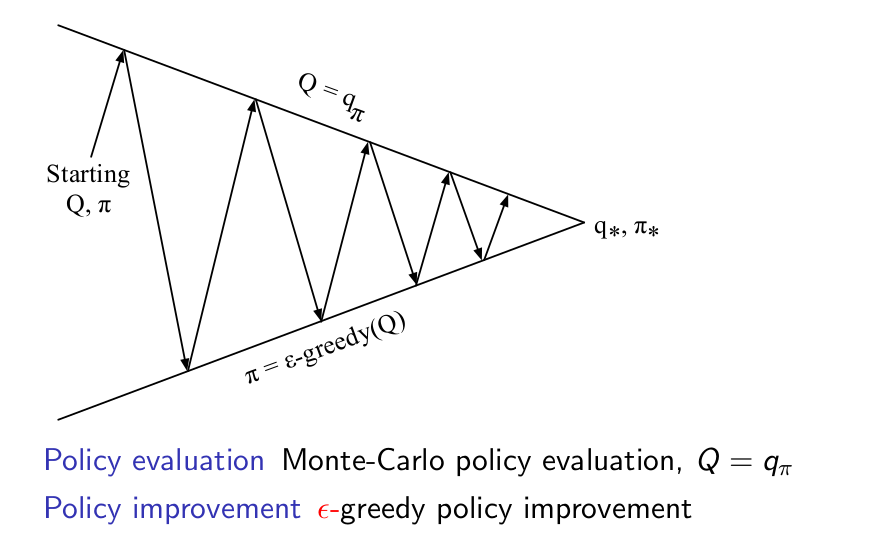
RewardHypothesis

On-Policy MC Control Without ES ($\epsilon$ soft Policy)

RewardHypothesis

On Policy vs Off Policy

Difference Between On-Policy and Off-Policy

RewardHypothesis

Issues with On-Policy Methods

  • Current Delimma:
    • learn action values conditional on subsequent optimal behavior,
    • but behave non-optimally in order to explore all actions (to find the optimal actions)
  • On-policy approach is actually a compromise:
    • learns action values not for the optimal policy, but for a near-optimal policy that still explores.

Off-Policy Learning

  • Use two policies,
    • one that is learned about and that becomes the optimal policy,
    • one that is more exploratory and is used to generate behavior.

  • Policy being learned about is called the target policy,

  • Policy used to generate behavior is called the behavior policy.

  • Hence, Learning is from data “off” the target policy, and the overall process is termed off-policy learning.

Off-Policy Learning

  • As the data is due to a different policy, off-policy methods are often

    • of greater variance and
    • are slower to converge.

  • off-policy methods are more powerful and general.(On-policy is a subset of Off-policy)

  • They can be applied to learn from data generated by a conventional non-learning controller, or from a human expert.

Off-Policy MC Prediction Methods

How to evaluate using off-policy methods?

  • We wish to estimate $v_\pi$ or $q_\pi$, but
    • Episodes following another policy $\mu$, where $\mu \neq \pi$.

  • Given $\pi$ is the target policy, $\mu$ is the behavior policy,

  • Both policies are considered fixed and given.

  • To evaluate action vaules following $\pi$ given episodes from following policy $\mu$ ,

    • off-policy methods utilize importance sampling,

  • Importance sampling: A general technique for estimating expected values under one distribution given samples from another.

  • Importance sampling: weight returns according to the relative probability of their trajectories under the target and behavior policies.
    • This ratio is called the importance-sampling ratio.

Importance Sampling

  • From $S_t$, the probability of the subsequent state–action trajectory, $A_t, S_{t+1}, A_{t+1},... , S_T$,
    • occurring under any policy $\pi$ is
      RewardHypothesis
  • The relative probability of the trajectory under the target and behavior policies (the importance-sampling ratio) is
RewardHypothesis
  • Importance sampling ratio ends up depending only on the two policies and not on the MDP.

Importance Sampling

1) Ordinary Importance Sampling

RewardHypothesis
2) Weighted Importance Sampling
RewardHypothesis

  • The ordinary importance-sampling estimator is unbiased whereas the weighted importance-sampling estimator is biased

  • The variance of the ordinary importance-sampling estimator is in general unbounded, whereas in the weighted estimator,assuming bounded returns, the variance of the weighted importance-sampling estimator converges to zero.

  • Weighted estimator usually has dramatically lower variance and is strongly preferred.

RewardHypothesis

Pseudocode: Off Policy MC Prediction

RewardHypothesis

Off Policy MC Control

Pseudocode: Off Policy MC Control

RewardHypothesis
** Return-Specific Importance Sampling** - Refer Sutton and Barto, Reinforcement learning: An introduction(Draft).

Summary

  • Monte Carlo Approach
  • On-Policy Prediction
    • On-Policy Control (w/o Assumption: Exploring Starts)
  • Off-Policy Prediction
    • Off-Policy Control
  • MC has several advantages over DP:
    • Can learn V and Q directly from interaction with environment
    • No need for full models
    • No need to learn about ALL states
  • MC methods provide an alternate policy evaluation process
    • No bootstrapping, i.e. updating not dependent on successor states (as opposed to DP)

One issue to watch for: maintaining sufficient exploration

  • exploring starts,
  • soft policies
  • off-policy methods