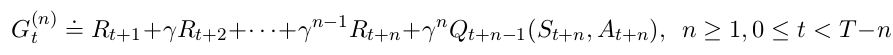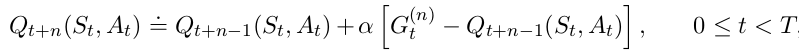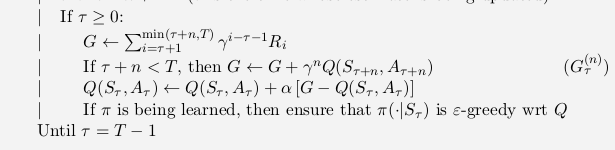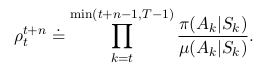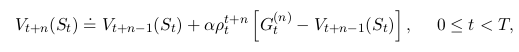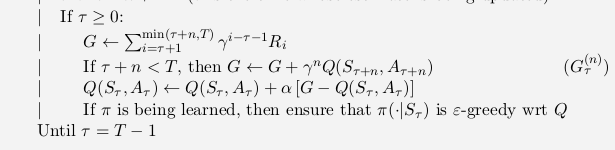Unifying MC Methods and TD Methods

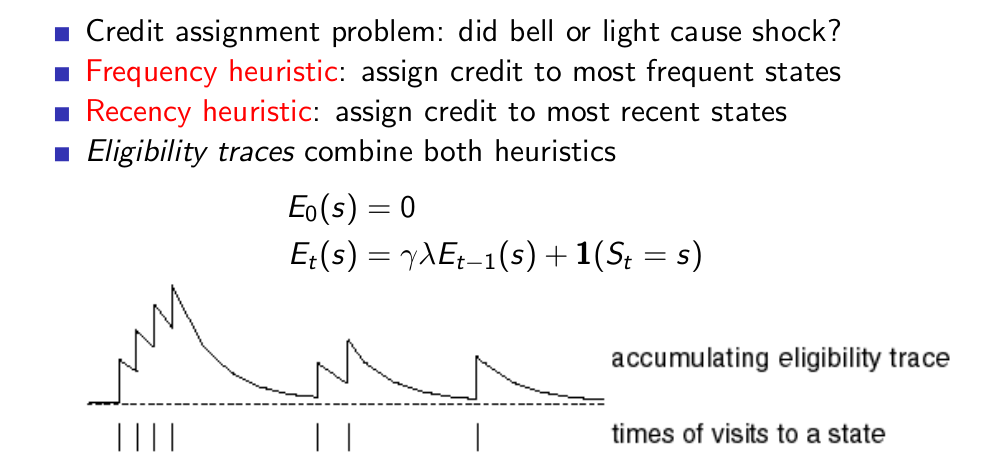
Bootstrapping, TD($\lambda$) and Eligibility Traces

Reference: Chapter 7 and Chapter 12, Sutton and Barto

Contents

• Bootstrapping

• TD ($\lambda$)

• Eligibility Traces

Bootstrapping

Bootstrapping and Sampling

Why do Bootstrapping?

• Free from tyranny of the time step
• Sometimes updates are required at every step of transition (one-step TD)
  • Take into account every possible transition/ anything that has changed
• Sometimes, it makes sense to only update every few stansitions (multi-step TD)
  • Take into account significant/considerable changes

n-Step Prediction

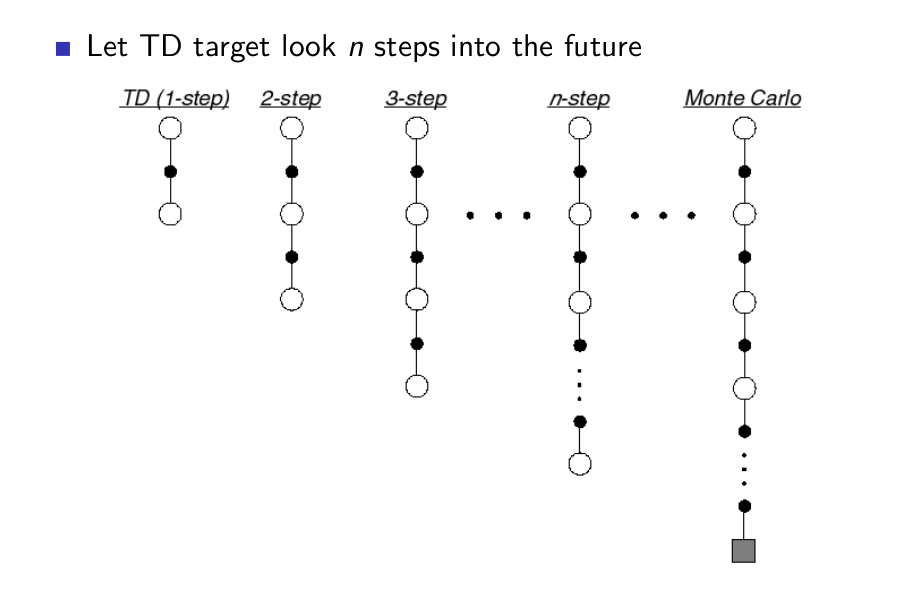
n-Step Return

n-Step Prediction

n-Step SARSA (On-Policy Control)

• simply switch states for actions (state–action pairs) and then use an $\epsilon$-greedy policy.
• The n-step returns in terms of estimated action values:
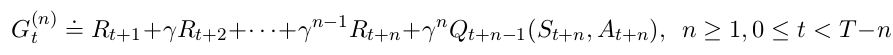
• Update made to a particular value of action-pair is as follows:

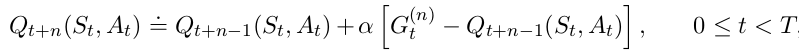
n-Step SARSA (On-policy Control)

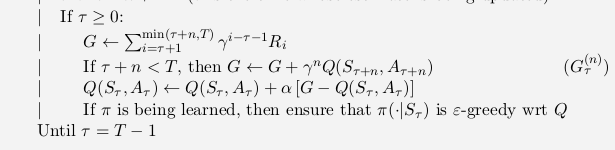
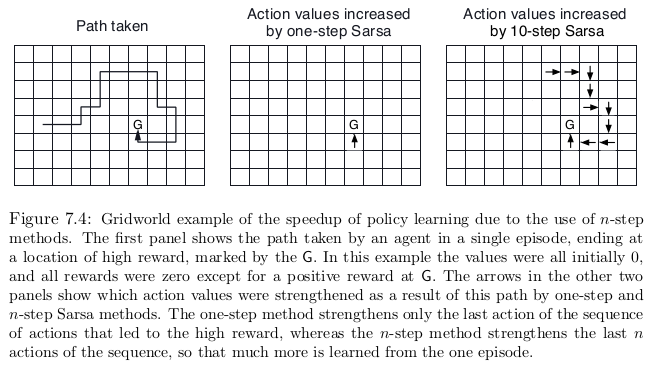
n-Step SARSA Example

n-Step Off-Policy Control (with Importance Sampling)

• learning the value function for one policy, π, while following another policy, μ
• Often, π is the greedy policy for the current action-value-function estimate, and μ is a more exploratory policy, perhaps ε-greedy
• we must take into account the difference between the two policies, using their relative probability of taking the actions that were taken
• To measure this difference, we use the importance sampling ratio.
• Only difference, that instead of measuring it for the entire episode, we measure it for n-steps.

• The importance sampling ratio looks liks:
• The update Equatin looks like this:

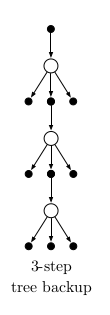
Off-Policy Control (w/o Importance Sampling => Tree BackUp Algorithm)

• This backup is an alternating mix of sample transitions—from each action to the su bsequent state—and full backups—from each state we consider all the possible actions, their probability of occuring under π, and their action values.

• Returns and updates are calculated as follows:

Unified view of Reinforcement Learning

TD($\lambda$)

Averaging n-Step Returns

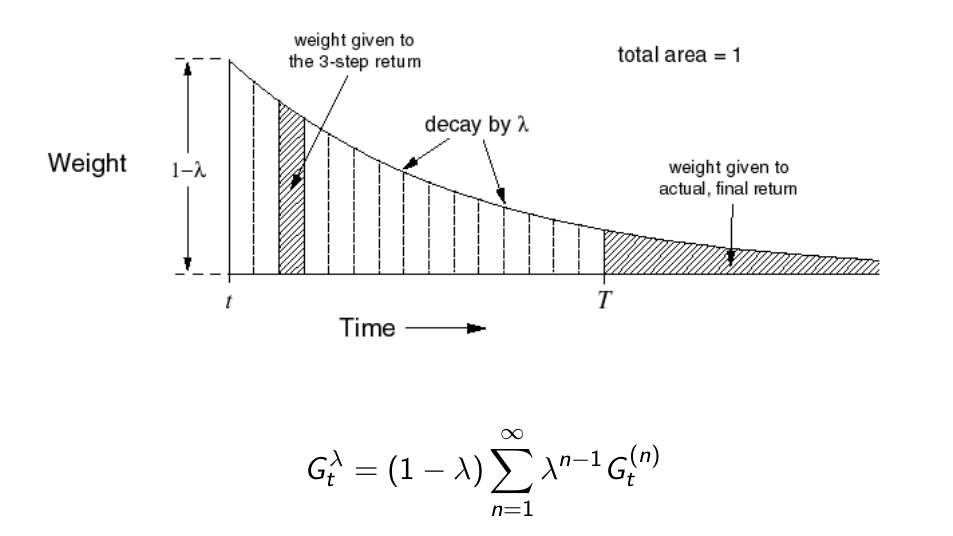
$\lambda$ Returns

TD(λ) Weighting Function

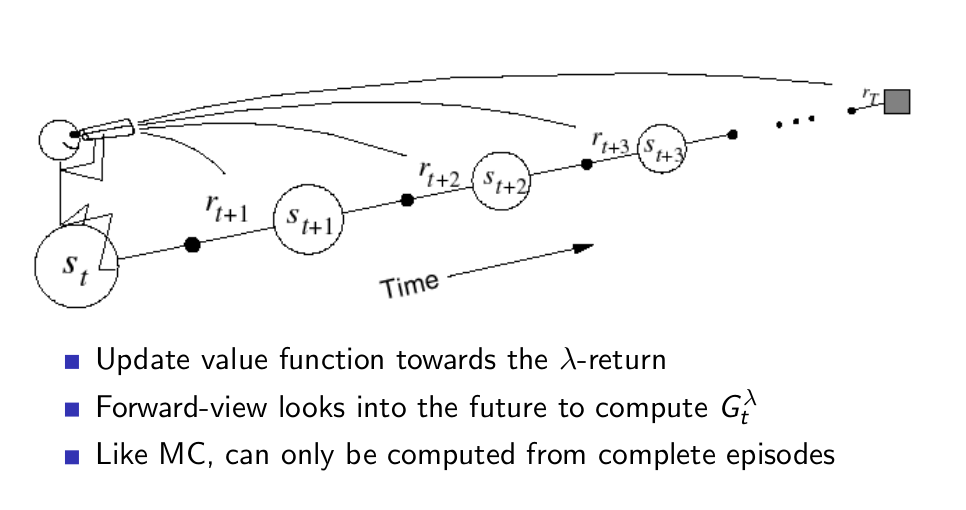
Forward-view TD(λ)

Bckward-view TD(λ)

Eligibility Traces

Eligibility Traces

Backward View TD(λ)

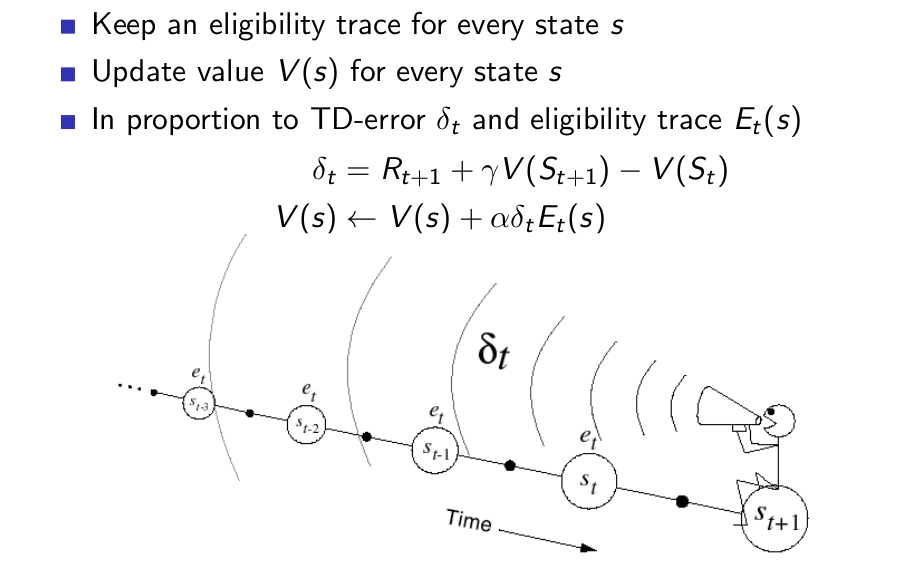
TD(λ) and TD(0)

TD(λ) and MC

MC and TD(1)

Telescoping in TD(1)

TD(λ) and TD(1)

Telescoping in TD(λ)

Forwards and Backwards TD(λ)

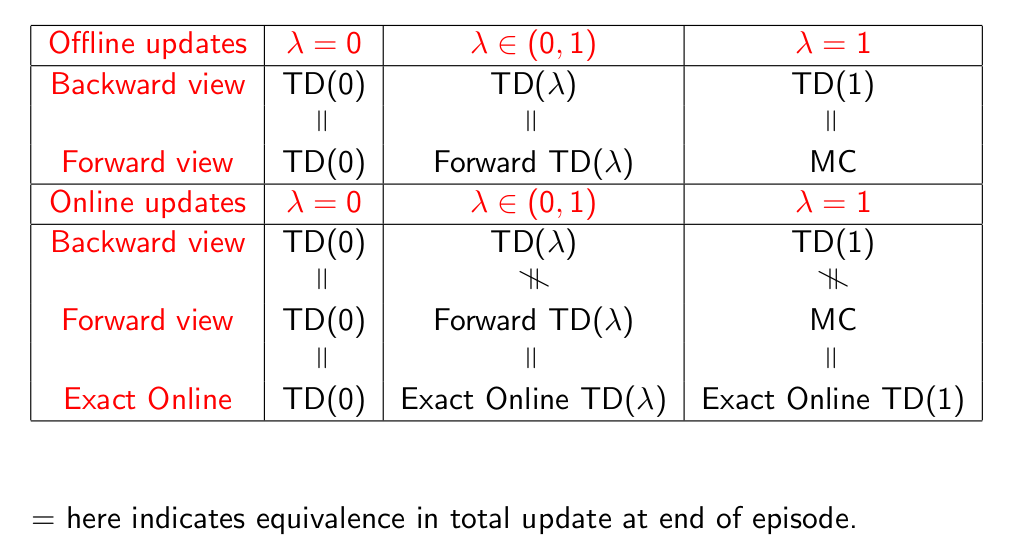
Offline Equivalence of Forward and Backward TD

Online Equivalence of Forward and Backward TD

Summary of Forward and Backward TD(λ)